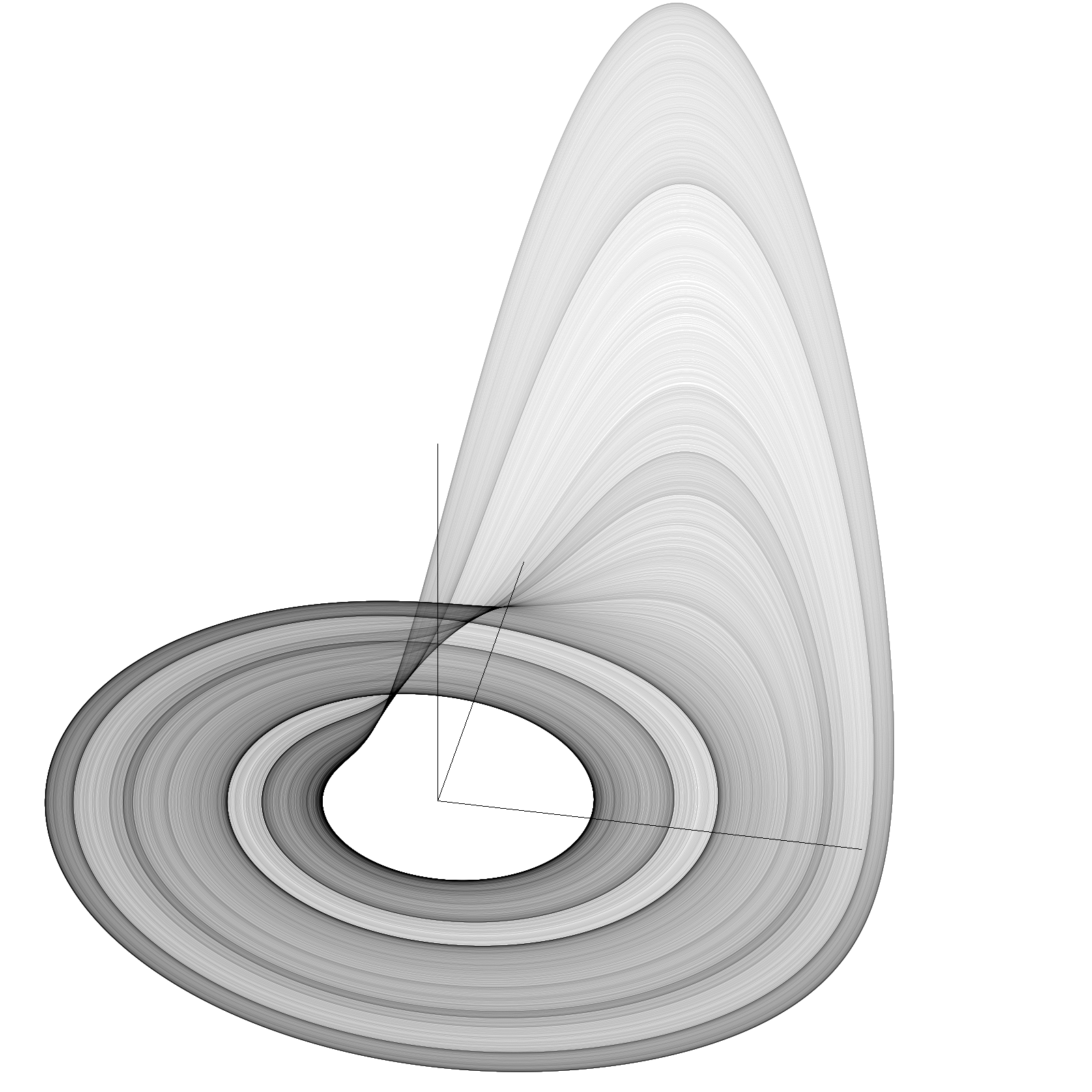
The Rössler system is a set of three non-linear ordinary differential equations that describe the behaviour of a simple chaotic system. The equations are named after the German physicist Otto Rössler, who introduced them in 1976.
The Rössler system is given by:
dx/dt = -y - z
dy/dt = x + ay
dz/dt = b + z(x-c)
Where x, y, and z are the state variables, and a, b, and c are parameters that control the behaviour of the system.
One of the key features of the Rössler system is that it exhibits chaotic behaviour for certain values of the parameters. This means that the system is highly sensitive to initial conditions, and small differences in the starting values of x, y, and z can lead to vastly different outcomes over time.
The Rössler system is also notable for its ability to produce strange attractors. A strange attractor is a geometric object that is associated with chaotic systems and serves as a visual representation of the system's behaviour. The Rössler attractor is a particularly simple and symmetric example of a strange attractor.
In addition to its mathematical and visual appeal, the Rössler system has applications in a variety of fields, including physics, chemistry, and engineering. It has been used to model the behaviour of chemical reactions, electronic circuits, and even the human heart.
Overall, the Rössler system is a simple but powerful tool for studying the behaviour of chaotic systems. Its ability to produce strange attractors and its wide range of applications make it a valuable tool for researchers and practitioners in a variety of fields.
We research, curate and publish daily updates from the field of AI.
Consider becoming a paying subscriber to get the latest!
