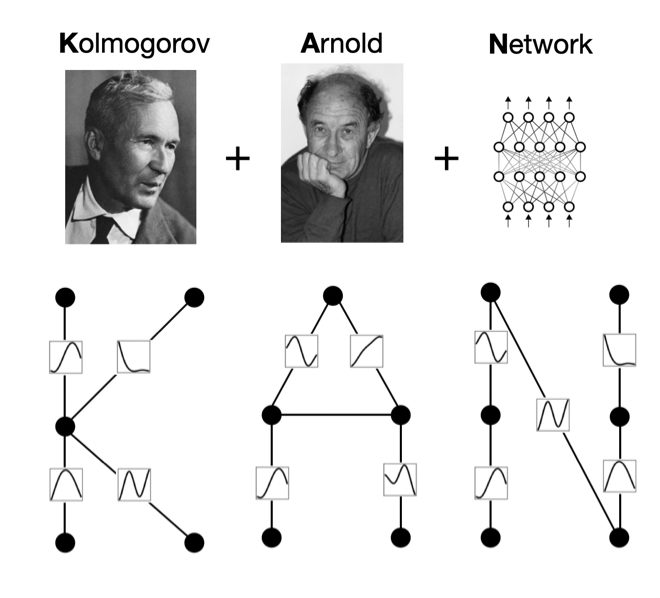
In recent years, the rise of deep learning has transformed many aspects of technology, from speech recognition systems to autonomous driving. However, traditional neural network architectures like Multi-Layer Perceptrons (MLPs) often come with limitations, particularly in terms of scalability, interpretability, and parameter efficiency. Enter Kolmogorov-Arnold Networks (KANs), a revolutionary architecture that promises to tackle these challenges head-on. This blog explores the innovative approach of KANs, comparing them with MLPs, and discussing their potential applications and benefits.
What are Kolmogorov-Arnold Networks?
Kolmogorov-Arnold Networks (KANs) are inspired by the Kolmogorov-Arnold representation theorem, a concept from mathematical analysis that asserts any multivariate continuous function can be represented as a composition of univariate functions and the addition operation. This theoretical foundation provides the bedrock for KANs, differentiating them significantly from the traditional MLPs which are based on the universal approximation theorem.
Unlike MLPs, which utilize fixed activation functions on nodes ("neurons"), KANs employ learnable activation functions on the edges ("weights") between nodes. This key change eliminates the use of linear weight matrices entirely. Instead, each weight parameter in KANs is replaced by a learnable univariate function, typically parametrized as a spline. This spline-based approach allows each "connection" within the network to dynamically adjust its processing function, promoting greater flexibility and efficiency.
Comparison with Multi-Layer Perceptrons
The introduction of KANs offers several enhancements over traditional MLPs:
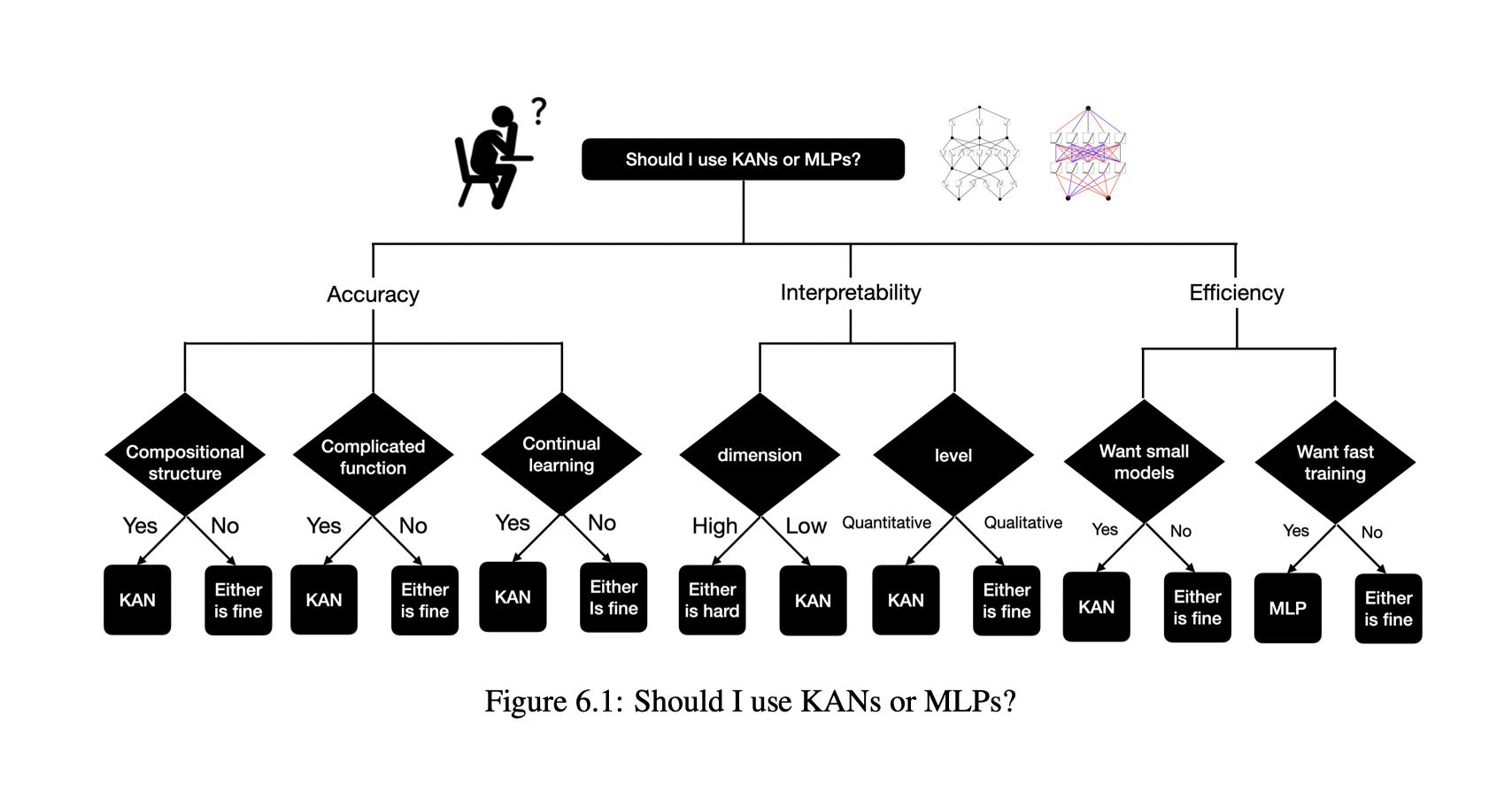
- Scalability and Efficiency: KANs demonstrate faster neural scaling laws, meaning they require significantly fewer parameters to achieve similar or superior performance compared to MLPs. For instance, in tasks such as solving partial differential equations (PDEs), KANs have shown to be 100 times more accurate and parameter-efficient than their MLP counterparts.
- Interpretability: One of the often-cited drawbacks of MLPs and other deep learning models is their "black box" nature. KANs, however, provide an architecture that is inherently more interpretable. The use of univariate functions as weights allows for easier visualization and understanding of what the network is doing, which is a significant advantage when deploying these models in real-world scenarios where trust and transparency are crucial.
- Accuracy: Empirical results have shown that KANs can outperform MLPs in accuracy, especially in applications involving data fitting and computational simulations. Their structure allows them to adapt more precisely to the intricacies of the input data.
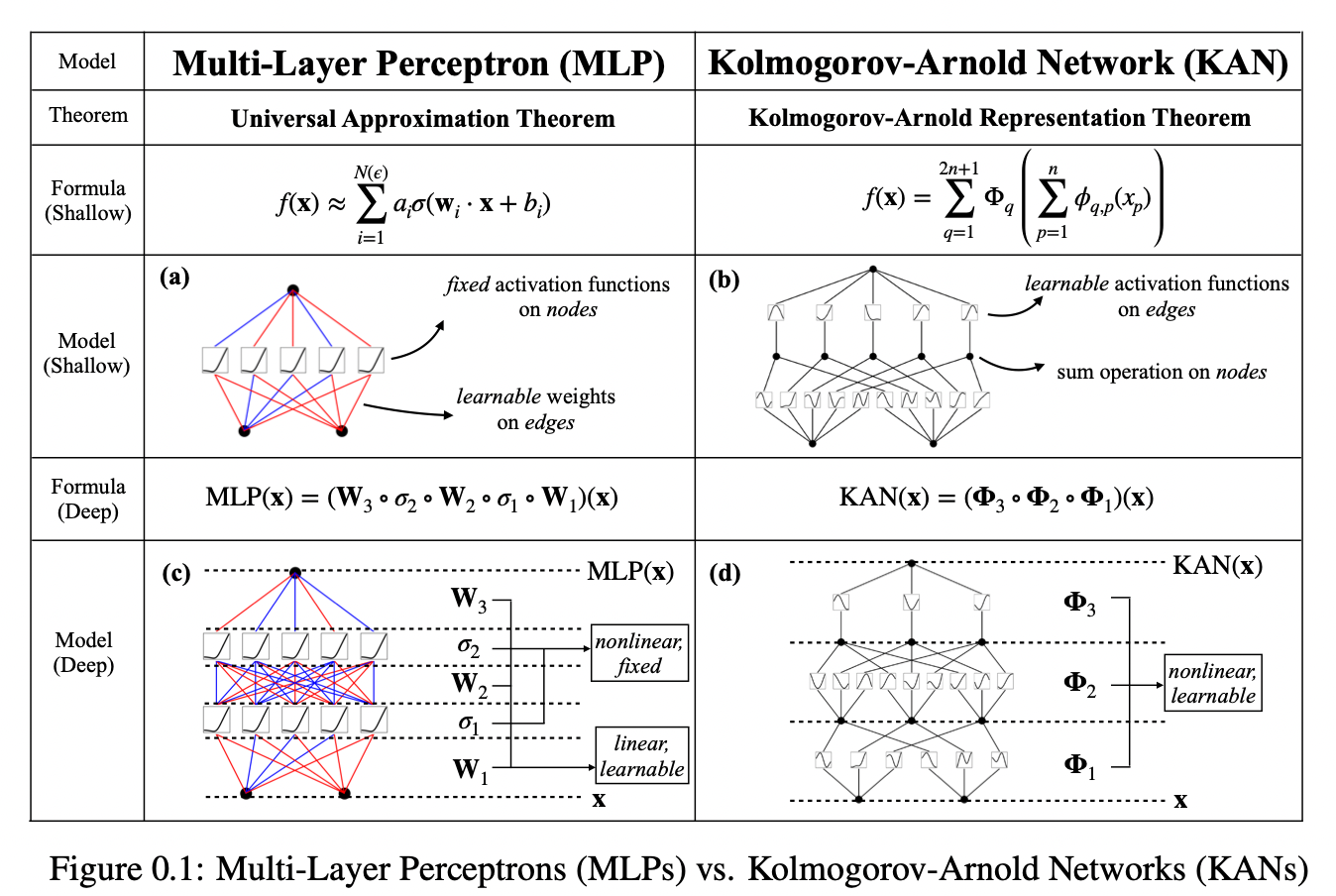
Despite their elegant mathematical interpretation, KANs are nothing more than combinations of splines and MLPs, leveraging their respective strengths and avoiding their respective weaknesses. Splines are accurate for low-dimensional functions, easy to adjust locally, and able to switch between different resolutions. However, splines have a serious curse of dimensionality (COD) problem, because of their inability to exploit compositional structures. MLPs, On the other hand, suffer less from COD thanks to their feature learning, but are less accurate than splines in low dimensions, because of their inability to optimize univariate functions. To learn a function accurately, a model should not only learn the compositional structure (external degrees of freedom), but should also approximate well the univariate functions (internal degrees of freedom). KANs are such models since they have MLPs on the outside and splines on the inside. As a result, KANs can not only learn features (thanks to their external similarity to MLPs), but can also optimize these learned features to great accuracy (thanks to their internal similarity to splines).
Practical Applications and Benefits
The flexibility and efficiency of KANs open up new possibilities in various fields. Here are a few areas where KANs can make a significant impact:
- Scientific Discovery: KANs have been demonstrated to be useful tools in the scientific process, helping researchers to rediscover mathematical and physical laws. This capability makes them valuable collaborators in the exploration of complex scientific problems.
- Enhanced Data Fitting: With their ability to model data more accurately with fewer parameters, KANs are ideal for fitting complex datasets in fields like finance, healthcare, and environmental science, where precision is paramount.
- Advanced Simulations: In areas requiring the solving of complex differential equations, such as climate modeling or engineering simulations, KANs provide a more efficient and accurate method than traditional techniques.
Read more: https://arxiv.org/pdf/2404.19756
Everyday Series is a newsletter for daily topics on AI. Aimed for both novice and professionals, it is delivered online, on email and over whatsapp.
